| LIBROW |
| Professional | Help | Support | Contacts |
Help 6.5
abs — absolute value function
1. Definition
Absolute value function is defined as
|x| = x for x ≥ 0;|x| = −x for x < 0.
2. Graph
Absolute value function is defined everywhere on real axis. Its graph is depicted below — fig. 1.
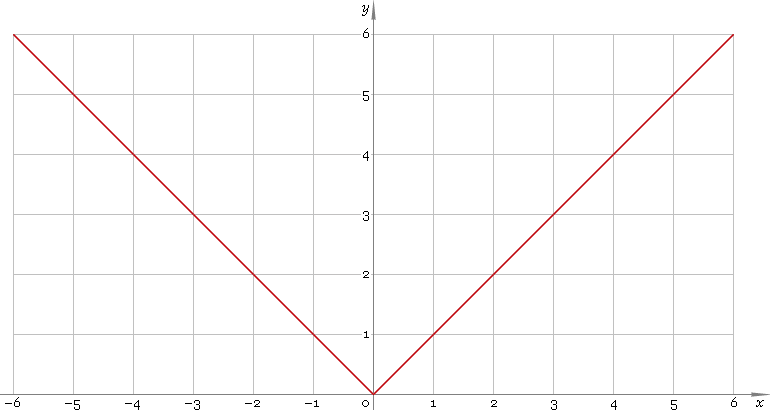 Fig. 1. Graph of the absolute value function y = |x|.
Fig. 1. Graph of the absolute value function y = |x|.
Function codomain is non-negative half of the real axis: [0, +∞).
3. Identities
Function is symmetrical:
|−x| = |x|Sum and difference of arguments:
|x + y| = |x| + |y|, if signx = signy|x + y| = ||x| − |y||, if signx ≠ signy
|x − y| = ||x| − |y||, if signx = signy
|x − y| = |x| + |y|, if signx ≠ signy
Product and ratio of arguments:
|xy| = |x||y||x /y| = |x| /|y|
4. Derivative and indefinite integral
Absolute value derivative:
|x|′ = 1 for x > 0;|x|′ = −1 for x < 0.
For 0 the derivative is undefined.
Indefinite integral of the absolute value:
∫ |x| dx = signx x2/2 + Cwhere sign is a signum function and C is an arbitrary constant.
5. How to use
To get absolute value of the number:
abs(−1);To calculate absolute value of the complex number:
abs(−1+i);To get absolute value of the current result:
abs(rslt);To get absolute value of the number z in calculator memory:
abs(mem[z]);6. Support
Absolute value of the real number is supported in free version of the Librow calculator.
Absolute value of the complex number is supported in professional version of the Librow calculator.
| Function 1 √ or sqrt |
|
| Function 2 Γ or Gamma |
|
| Function 3 ∏ or Prod |
|
| Function 4 ∑ or Sum |
|
| Function 5 abs |
|
| Function 6 arccos |
|
| Function 7 arccot or arcctg |
|
| Function 8 arccsc or arccosec |
|
| Function 9 arcosh or arch |
|
| Function 10 arcoth or arcth |
|
| Function 11 arcsch |
|
| Function 12 arcsec |
|
| Function 13 arcsin |
|
| Function 14 arctan or arctg |
|
| Function 15 arg |
|
| Function 16 arsech or arsch |
|
| Function 17 arsinh or arsh |
|
| Function 18 artanh or arth |
|
| Function 19 ceil |
|
| Function 20 conj |
|
| Function 21 cos |
|
| Function 22 cosh or ch |
|
| Function 23 cot or ctg |
|
| Function 24 coth or cth |
|
| Function 25 csc or cosec |
|
| Function 26 csch |
|
| Function 27 exp |
|
| Function 28 fact |
|
| Function 29 floor |
|
| Function 30 I |
|
| Function 31 im |
|
| Function 32 J |
|
| Function 33 K |
|
| Function 34 ln |
|
| Function 35 log or lg |
|
| Function 36 ^ |
|
| Function 37 rand |
|
| Function 38 re |
|
| Function 39 sec |
|
| Function 40 sech |
|
| Function 41 sign |
|
| Function 42 sin |
|
| Function 43 sinh or sh |
|
| Function 44 tan or tg |
|
| Function 45 tanh or th |
|
| Function 46 Y |
|
|||||||||||||
|
|||||||||||||