| LIBROW |
| Professional | Help | Support | Contacts |
Help 6.33
K — modified Bessel function of the second kind
1. Definition
By definition modified Bessel function is solution of the modified Bessel equation
z2 w′′ + z w′ − (z2 + ν2) w = 0As second order equation it has two solutions, second of which has singularity at 0 and is called modified Bessel function of the second kind — Kν. Parameter ν is called order of the function.
First solution has no singularity at 0 and is called modified Bessel function of the first kind — Iν.
2. Graph
Modified Bessel functions of the second kind defined everywhere on the real axis, at 0 functions have singularity, so their domain is (−∞, 0)∪(0, +∞). Graphs of the first three representatives of the second kind modified Bessel function family depicted below — fig. 1.
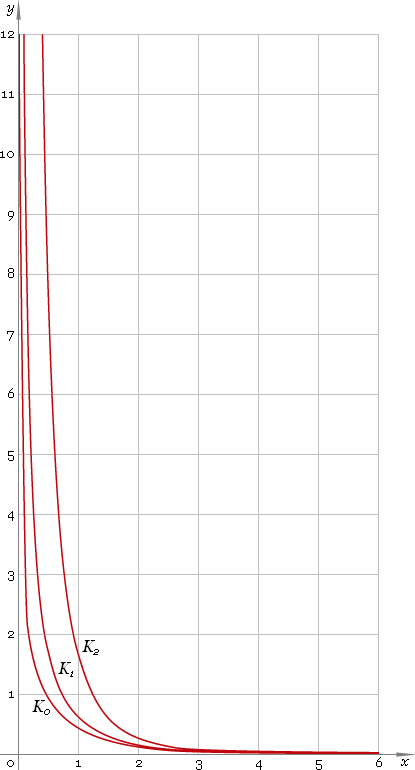 Fig. 1. Graphs of the modified Bessel functions of the second kind y = K0(x), y = K1(x) and y = K2(x).
Fig. 1. Graphs of the modified Bessel functions of the second kind y = K0(x), y = K1(x) and y = K2(x).
3. Identities
Connection to the ordinary Bessel functions:
Kν(z) = π /2 iν+1[Jν(iz) + iYν(iz)]Connection to the modified Bessel function of the first kind:
Kν(z) = π / [2 sin(πν)] [I−ν(z) − Iν(z)]Next order recurrence:
Kν+1(z) = 2ν /z Kν(z) + Kν−1(z)Negative argument:
Kν(−z) = e−iπν Kν(z) − i π Iν(z) = cos(πν) Kν(z) − i [sin(πν) Kν(z) + π Iν(z)]For the case of integer order ν=n the negative argument identity can be simplified down to:
Kn(−z) = (−1)n Kn(z) − i π In(z)and for the case of half-integer order ν=n+1/2 the identity can be simplified down to:
Kn+1/2(−z) = −i [(−1)n Kn+1/2(z) + π In+1/2(z)]Reflection — negative order:
K−ν(z) = Kν(z)4. Derivative
Modified Bessel function of the second kind derivative:
K′ν(z) = −Kν−1(z) − ν Kν(z) /z K′ν(z) = ν Kν(z) /z − Kν+1(z) K′ν(z) = −[Kν−1(z) + Kν+1(z)] /2In particular:
K′0(z) = −K1(z)5. Interface
Modified Bessel function call looks like
K(ν, z);where ν is the function real order, and z — function complex argument.
6. How to use
To calculate modified Bessel function of the second kind of the 0 order of the number:
K(0, 1.5−i);To get modified Bessel function of the second kind of the 1.2 order of the current result:
K(1.2, rslt);To get modified Bessel function of the second kind of the 2.5 order of the number z in calculator memory:
K(2.5, mem[z]);7. Support
Modified Bessel function of the second kind of real order and complex argument is supported in professional version of the Librow calculator.
| Function 1 √ or sqrt |
|
| Function 2 Γ or Gamma |
|
| Function 3 ∏ or Prod |
|
| Function 4 ∑ or Sum |
|
| Function 5 abs |
|
| Function 6 arccos |
|
| Function 7 arccot or arcctg |
|
| Function 8 arccsc or arccosec |
|
| Function 9 arcosh or arch |
|
| Function 10 arcoth or arcth |
|
| Function 11 arcsch |
|
| Function 12 arcsec |
|
| Function 13 arcsin |
|
| Function 14 arctan or arctg |
|
| Function 15 arg |
|
| Function 16 arsech or arsch |
|
| Function 17 arsinh or arsh |
|
| Function 18 artanh or arth |
|
| Function 19 ceil |
|
| Function 20 conj |
|
| Function 21 cos |
|
| Function 22 cosh or ch |
|
| Function 23 cot or ctg |
|
| Function 24 coth or cth |
|
| Function 25 csc or cosec |
|
| Function 26 csch |
|
| Function 27 exp |
|
| Function 28 fact |
|
| Function 29 floor |
|
| Function 30 I |
|
| Function 31 im |
|
| Function 32 J |
|
| Function 33 K |
|
| Function 34 ln |
|
| Function 35 log or lg |
|
| Function 36 ^ |
|
| Function 37 rand |
|
| Function 38 re |
|
| Function 39 sec |
|
| Function 40 sech |
|
| Function 41 sign |
|
| Function 42 sin |
|
| Function 43 sinh or sh |
|
| Function 44 tan or tg |
|
| Function 45 tanh or th |
|
| Function 46 Y |
|
|||||||||||||
|
|||||||||||||