| LIBROW |
| Professional | Help | Support | Contacts |
Help 6.19
ceil — ceiling function
1. Definition
Ceiling is the nearest integer to the righ — the smallest integer greater than or equal to the argument.
2. Graph
The ceiling function is defined everywhere on the real axis — so its domain is (−∞, +∞). Its stair-like graph is depicted below — fig. 1.
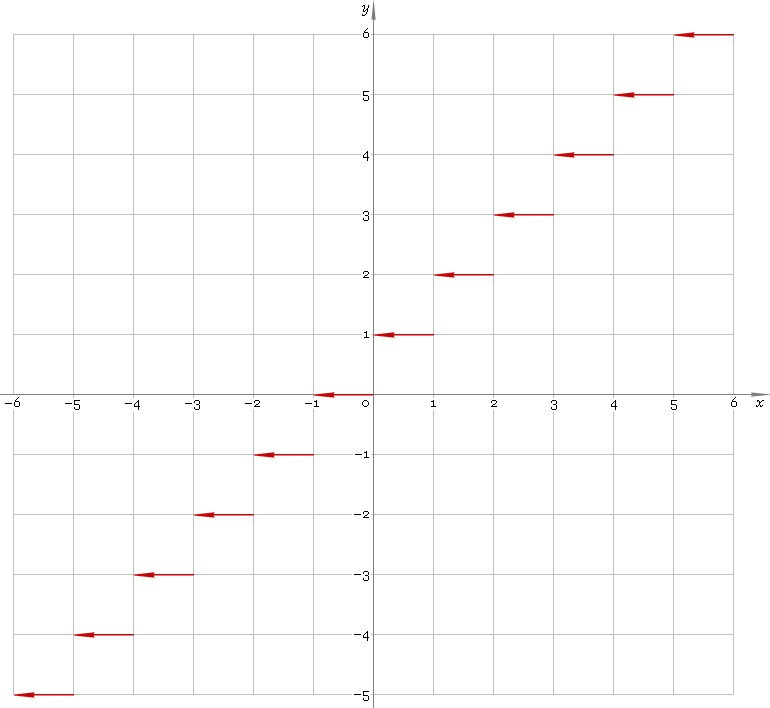 Fig. 1. Graph of the ceiling function y = ceilx.
Fig. 1. Graph of the ceiling function y = ceilx.
The function codomain is the set of integer numbers.
3. How to use
To calculate the ceiling of the number:
ceil(−1.8);To get the ceiling of the complex number:
ceil(−1.8+i*1.2);To get the ceiling of the current result:
ceil(rslt);To get the ceiling of the number z in calculator memory:
ceil(mem[z]);4. Support
The ceiling function of the complex argument is supported in the professional version of the Librow calculator.
| Function 1 √ or sqrt |
|
| Function 2 Γ or Gamma |
|
| Function 3 ∏ or Prod |
|
| Function 4 ∑ or Sum |
|
| Function 5 abs |
|
| Function 6 arccos |
|
| Function 7 arccot or arcctg |
|
| Function 8 arccsc or arccosec |
|
| Function 9 arcosh or arch |
|
| Function 10 arcoth or arcth |
|
| Function 11 arcsch |
|
| Function 12 arcsec |
|
| Function 13 arcsin |
|
| Function 14 arctan or arctg |
|
| Function 15 arg |
|
| Function 16 arsech or arsch |
|
| Function 17 arsinh or arsh |
|
| Function 18 artanh or arth |
|
| Function 19 ceil |
|
| Function 20 conj |
|
| Function 21 cos |
|
| Function 22 cosh or ch |
|
| Function 23 cot or ctg |
|
| Function 24 coth or cth |
|
| Function 25 csc or cosec |
|
| Function 26 csch |
|
| Function 27 exp |
|
| Function 28 fact |
|
| Function 29 floor |
|
| Function 30 I |
|
| Function 31 im |
|
| Function 32 J |
|
| Function 33 K |
|
| Function 34 ln |
|
| Function 35 log or lg |
|
| Function 36 ^ |
|
| Function 37 rand |
|
| Function 38 re |
|
| Function 39 sec |
|
| Function 40 sech |
|
| Function 41 sign |
|
| Function 42 sin |
|
| Function 43 sinh or sh |
|
| Function 44 tan or tg |
|
| Function 45 tanh or th |
|
| Function 46 Y |
|
|||||||||||||
|
|||||||||||||