| LIBROW |
| Professional | Help | Support | Contacts |
Help 6.12
arcsec — trigonometric arc secant function
1. Definition
Arc secant is inverse of the secant function.
arcsecx ≡ secinvx2. Graph
Arc secant is discontinuous function defined on all real axis except the (−1, 1) range — so its domain is (−∞, −1]∪[1, +∞). Function graph is depicted below — fig. 1.
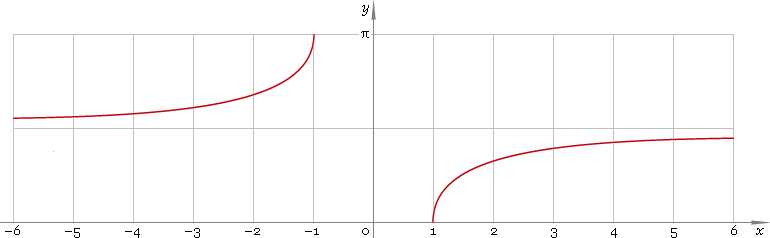 Fig. 1. Graph of the arc secant function y = arcsecx.
Fig. 1. Graph of the arc secant function y = arcsecx.
Function codomain is limited to the range [0, π/2)∪(π/2, π].
3. Identities
Complementary angle:
arcsecx + arccscx = π/2and as consequence:
arcsec csc φ = π/2 − φNegative argument:
arcsec(−x) = π − arcsecxReciprocal argument:
arsec(1/x) = arccosxSum and difference:
arcsecx + arcsecy = arcsec(xy /{1 − xy√[(1 − 1 /x2)(1 − 1 /y2)]})arcsecx − arcsecy = arcsec(xy /{1 + xy√[(1 − 1 /x2)(1 − 1 /y2)]})
Some argument values:
| Argument x | Value arcsecx |
|---|---|
| 1 | 0 |
| √6 − √2 | π/12 |
| √(50 − 10√5) /5 | π/10 |
| √(2 − √2) | π/8 |
| 2√3 /3 | π/6 |
| √5 − 1 | π/5 |
| √2 | π/4 |
| √(50 + 10√5) /5 | 3π/10 |
| 2 | π/3 |
| √(4 + 2√2) | 3π/8 |
| √5 + 1 | 2π/5 |
| √6 + √2 | 5π/12 |
4. Derivative and indefinite integral
Arc secant derivative:
arcsec′x = 1 /[|x| √(x2 − 1)]Indefinite integral of the arc secant:
∫ arcsecx dx = x arcsecx − signx ln|x + √(x2 − 1)| + C = x arcsecx − arcosh|x| + Cwhere sign is a signum function and C is an arbitrary constant.
5. How to use
To calculate arc secant of the number:
arcsec(−1);To get arc secant of the complex number:
arcsec(−1−i);To get arc secant of the current result:
arcsec(rslt);To get arc secant of the number z in calculator memory:
arcsec(mem[z]);6. Support
Trigonometric arc secant of the real argument is supported in free version of the Librow calculator.
Trigonometric arc secant of the complex argument is supported in professional version of the Librow calculator.
| Function 1 √ or sqrt |
|
| Function 2 Γ or Gamma |
|
| Function 3 ∏ or Prod |
|
| Function 4 ∑ or Sum |
|
| Function 5 abs |
|
| Function 6 arccos |
|
| Function 7 arccot or arcctg |
|
| Function 8 arccsc or arccosec |
|
| Function 9 arcosh or arch |
|
| Function 10 arcoth or arcth |
|
| Function 11 arcsch |
|
| Function 12 arcsec |
|
| Function 13 arcsin |
|
| Function 14 arctan or arctg |
|
| Function 15 arg |
|
| Function 16 arsech or arsch |
|
| Function 17 arsinh or arsh |
|
| Function 18 artanh or arth |
|
| Function 19 ceil |
|
| Function 20 conj |
|
| Function 21 cos |
|
| Function 22 cosh or ch |
|
| Function 23 cot or ctg |
|
| Function 24 coth or cth |
|
| Function 25 csc or cosec |
|
| Function 26 csch |
|
| Function 27 exp |
|
| Function 28 fact |
|
| Function 29 floor |
|
| Function 30 I |
|
| Function 31 im |
|
| Function 32 J |
|
| Function 33 K |
|
| Function 34 ln |
|
| Function 35 log or lg |
|
| Function 36 ^ |
|
| Function 37 rand |
|
| Function 38 re |
|
| Function 39 sec |
|
| Function 40 sech |
|
| Function 41 sign |
|
| Function 42 sin |
|
| Function 43 sinh or sh |
|
| Function 44 tan or tg |
|
| Function 45 tanh or th |
|
| Function 46 Y |
|
|||||||||||||
|
|||||||||||||