| LIBROW |
| Professional | Help | Support | Contacts |
Help 6.34
ln — natural logarithmic function
1. Definition
Natural logarithmic function is the inverse of the exponential function.
2. Graph
Natural logarithmic function is defined on positive part of the real axis — so its domain is (0, +∞). 0 is a singular point. Function graph is depicted below — fig. 1.
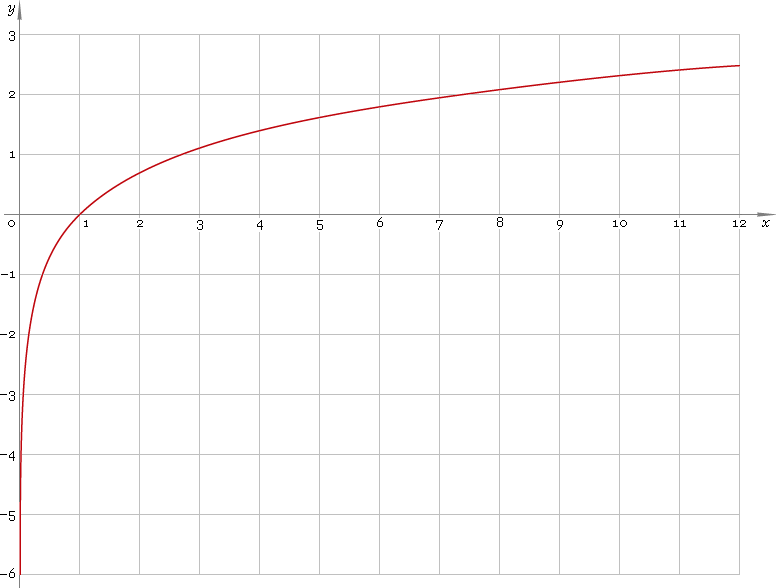 Fig. 1. Graph of the natural logarithmic function y = lnx.
Fig. 1. Graph of the natural logarithmic function y = lnx.
Function codomain is entire real axis.
3. Identities
By definition:
ln ex ≡ xReciprocal argument:
ln(1/x) = −lnxProduct and ratio of arguments:
ln(xy) = lnx + lnyln(x /y) = lnx − lny
Power of argument:
lnxa = a lnxBase change:
logax = lnx /lnalogax = logbx /logba
4. Derivative and indefinite integral
Natural logarithm derivative:
ln′x = 1 /xAs well:
ln′|x| = 1 /xIndefinite integral of the natural logarithm:
∫ lnx dx = x lnx − x + Cwhere C is an arbitrary constant.
5. How to use
To calculate natural logarithm of the number:
ln(2);To get natural logarithm of the complex number:
ln(2+i);To get natural logarithm of the current result:
ln(rslt);To get natural logarithm of the number z in calculator memory:
ln(mem[z]);6. Support
Natural logarithm of the real argument is supported in free version of the Librow calculator.
Natural logarithm of the complex argument is supported in professional version of the Librow calculator.
| Function 1 √ or sqrt |
|
| Function 2 Γ or Gamma |
|
| Function 3 ∏ or Prod |
|
| Function 4 ∑ or Sum |
|
| Function 5 abs |
|
| Function 6 arccos |
|
| Function 7 arccot or arcctg |
|
| Function 8 arccsc or arccosec |
|
| Function 9 arcosh or arch |
|
| Function 10 arcoth or arcth |
|
| Function 11 arcsch |
|
| Function 12 arcsec |
|
| Function 13 arcsin |
|
| Function 14 arctan or arctg |
|
| Function 15 arg |
|
| Function 16 arsech or arsch |
|
| Function 17 arsinh or arsh |
|
| Function 18 artanh or arth |
|
| Function 19 ceil |
|
| Function 20 conj |
|
| Function 21 cos |
|
| Function 22 cosh or ch |
|
| Function 23 cot or ctg |
|
| Function 24 coth or cth |
|
| Function 25 csc or cosec |
|
| Function 26 csch |
|
| Function 27 exp |
|
| Function 28 fact |
|
| Function 29 floor |
|
| Function 30 I |
|
| Function 31 im |
|
| Function 32 J |
|
| Function 33 K |
|
| Function 34 ln |
|
| Function 35 log or lg |
|
| Function 36 ^ |
|
| Function 37 rand |
|
| Function 38 re |
|
| Function 39 sec |
|
| Function 40 sech |
|
| Function 41 sign |
|
| Function 42 sin |
|
| Function 43 sinh or sh |
|
| Function 44 tan or tg |
|
| Function 45 tanh or th |
|
| Function 46 Y |
|
|||||||||||||
|
|||||||||||||